NLP Lecture 1
Hidden Markov Model
HMM 模型有以下的基本假设:
- 系统在每一个时刻 \(i\) 处于一个隐藏状态 \(q_i\),当前状态只与前一个状态相关;
- 在每一个隐藏状态 \(q_i\) 下,系统会产生一个可观测的输出 \(o_i\).
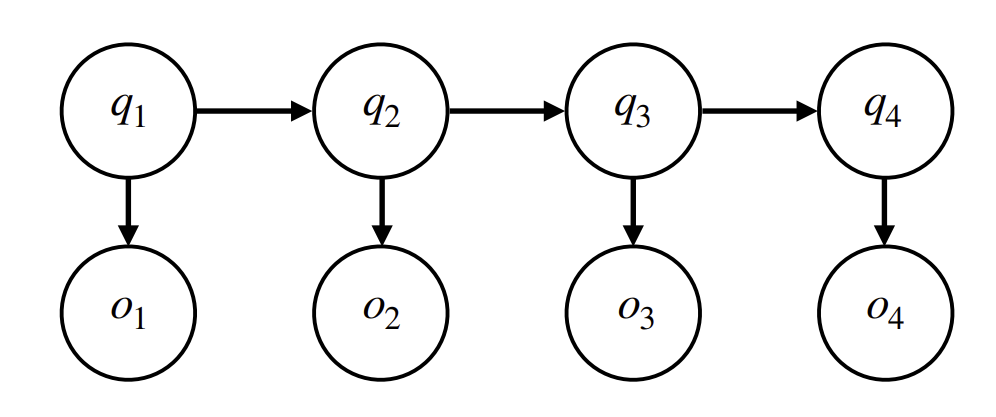
在这一假设下,产生了模型的各个部分:
- 状态序列:表示隐含的标注状态,在 POS 标注任务中,状态就是每个词的词性。
- 比如名词、动词等。
- 观测序列:表示可观测的输出序列,在 POS 标注中,观测序列就是句子中的词。
- 初始概率分布:模型在第一个时间步(句子中的第一个词)处于某个状态的概率。
- 状态转移概率:当前状态转移到下一个状态的概率,表示了词性序列之间的相互关系。
- 例如,动词后面更有可能是名词还是另一个动词?
- 发射概率:在给定某个状态的情况下,生成特定观测值的概率。
- 例如,给定状态为名词,出现 “interest” 这个词的概率是多少?
在这一模型下,我们可以表示通过隐藏态 \(Q=\left(q_1,q_2,\cdots,q_n\right)\),一个句子 \(O=\left(o_1,o_2,\cdots,o_n\right)\) 被生成的概率: \[ \begin{aligned} p\left(Q, O\right) &= p\left(q_1\right) \cdot p\left(q_2 \mid q_1\right) \cdot p\left(q_3 \mid q_2\right) \cdot ... \cdot p\left(q_n \mid q_{n-1}\right) \cdot p\left(o_1 \mid q_1\right) \cdot p\left(o_2 \mid q_2\right) \cdot ... \cdot p\left(o_n \mid q_n\right)\\ &= p\left(q_1\right)\cdot\left(\prod_{t=2}^{n}p\left(q_t\mid q_{t-1}\right)\right)\cdot\left(\prod_{t=1}^{n}p\left(o_t\mid q_t\right)\right). \end{aligned} \]
如果我们重点关心句子中各个词的局部关系,就可以使用 HMM 来对句子的每一个成分进行词汇标注。
任务:给定一个句子(观测序列),我们希望通过 HMM 模型来预测每个单词的词性(隐藏状态序列)。例如,在句子 "Fed raises interest rates \(0.5\) percent" 中,句子中的单词作为输入,我们希望输出每个单词的词性,这里期望的答案为 "Fed" 是名词,"raises" 是动词,"interest" 是名词,依此类推。
与随机游走的方向不同,在词性标注任务中,我们先知道观测值 \(O\) (也就是句子中的单词),然后需要根据 \(O\) 推断出对应的隐藏状态序列 \(Q\) 是什么(即每个单词的词性)。显然这个状态有多种可能,因此我们采用最大似然估计去求“最可能”的 \(Q\) 是什么: \[ Q_{ans}=\arg\max_{Q}p\left(Q\mid O\right). \] 由于 \[ p\left(Q\mid O\right)=\frac{p\left(Q,O\right)}{p\left(O\right)} \] 而对于一个训练好的 HMM, \(P\left(O\right)\) 已经是定值,因此 \(\arg\max_{Q}p\left(Q\mid O\right)=\arg\max_{Q}p\left(Q, O\right)\),我们进而处理后者即可。为了计算它,我们介绍 Forward & Backward Algorithm 来解决这个问题。
Forward Algorithm
因马尔可夫过程的下一状态只和前一状态有直接关系,故设计如下的递推形式来计算:\(p\left(O_{:t},q_t=j\right)\),也就是在时刻 \(t\) 时,HMM 生成的前 \(t\) 项观测序列和我们输入的序列 \(O\) 重合的概率。
根据递推关系,我们可以写出 \[ p\left(O_{:t}, q_t = j\right) = p\left(o_t \mid q_t = j\right) \cdot \sum_{i} \left[ p\left(O_{:t-1}, q_{t-1} = i\right) \cdot p\left(q_t = j \mid q_{t-1} = i\right) \right] \] 递推关系的解释:前 \(t-1\) 项确定后,对第 \(t-1\) 时刻状态讨论。
用 \(\alpha\left(t,j\right)\) 来表示 \(p\left(O_{:t}, q_t = j\right)\),我们可以将上面的递推式简写为 \[ \begin{cases} \displaystyle\alpha\left(t,j\right)=b_j\left(o_t\right)\sum_{i}\alpha\left(t,j-1\right)\,a_{ij}, &t\geq2\\ \displaystyle\alpha\left(1,j\right)=\pi_j\,b_j\left(o_1\right), &t=1 \end{cases} \]
这就将 \(\alpha\left(t,j\right)\) 的计算转化成了动态规划问题。其中 \(b_j\left(o_t\right)\) 是 \(j\) 状态的发射概率,\(a_{ij}\) 是状态转移矩阵的 \(\left(i,j\right)\) 项。
随后可以计算出 \[ p\left(O\right)=\sum_{i}p\left(O_{:n},q_n=i\right)=\sum_{i}\alpha\left(n,i\right), \] 复杂度是 \(O\left(mn^2\right)\),\(n\) 是长度,\(m\) 是状态数量。
Backward Algorithm
前向算法计算了 \(p\left(O_{:t}, q_t = j\right)\) ,后向算法负责处理另外一部分 \(p\left(O_{t+1:} \mid q_t = i\right)\) 的计算,也就是在时刻 \(t\) 观察到状态 \(q_t=i\) 后,从第 \(t+1\) 项开始之后都与输入序列对应位置一样的概率。
同样可以列出递推式 \[ p\left(O_{t+1:} \mid q_t = i\right) = \sum_j\big(p\left(q_{t+1} = j \mid q_t = i\right)\cdot p\left(o_{t+1} \mid q_{t+1} = j\right)\cdot p\left(O_{t+2:}, q_{t+1} = j\right)\big) \] 递推关系的解释:关注第 \(t+1\) 项的后面,对第 \(t+2\) 时刻的状态讨论。注意这里都是条件概率,条件是 \(q_t=i\)。
用 \(\beta\left(t, i\right)\) 表示 \(p\left(O_{t+1:} \mid q_t = i\right)\),我们可以将上面的递推式简写为 \[ \begin{cases} \displaystyle\beta\left(t,i\right)=\sum_j a_{ij}\,b_j\left(o_{t+1}\right) \beta\left(t+1, j\right), &t<n\\ \beta\left(n, i\right) = 1, &t=n \end{cases} \] 同样转化为动态规划问题。
现在我们已经计算出
\[ \begin{aligned} \alpha\left(t, i\right) &= p\left(O_{:t}, q_t = i\right)\\ \beta\left(t, i\right) &= p\left(O_{t+1:} \mid q_t = i\right) \end{aligned} \] 结合后,可以计算: \[ \alpha\left(t, i\right) \beta\left(t, i\right) = p\left(O, q_t = i\right) \] 以及 \[ \begin{aligned} p\left(O, q_t = i, q_{t+1} = j\right) &=p\left(O_{:t}, q_t = i\right)\cdot p\left(q_{t+1}=j\mid q_t = i\right)\cdot p\left(o_{t+1}\mid q_{t+1}=j\right)\cdot p\left(O_{t+2:} \mid q_{t+1} = j\right)\\ &=\alpha\left(t, i\right)\,a_{ij}\,b_j\left(o_{t+1}\right)\,\beta\left(t+1, j\right)\\ \end{aligned} \] 备注:\(p\left(O_{t+1:} \mid q_t = i\right)=p\left(O_{t+1:} \mid q_t = i,O_{:t}\right)\).
寻找最优的 \(Q\): Viterbi 算法
Viterbi 算法使用动态规划来计算给定观察序列下最有可能的状态序列: \[ \begin{aligned} &\phantom{=}\max_{Q_{:t-1}} p\left(O_{:t}, Q_{:t-1}, q_t = j\right)\\ &= \max_i \left( \max_{Q_{:t-2}} p\left(O_{:t-1}, Q_{:t-2}, q_{t-1} = i\right) \cdot p\left(q_t = j \mid q_{t-1} = i\right) \cdot p\left(o_t \mid q_t = j\right) \right) \end{aligned} \] 其中 \(\displaystyle\max_{Q_{:t-1}} p\left(O_{:t}, Q_{:t}\right)\) 被分解成各个 \(\displaystyle\max_{Q_{:t-1}} p\left(O_{:t}, Q_{:t-1}, q_t = j\right)\) 以建立递推关系。“最大值”的递推关系是有公式本身的形式决定的: \[ \begin{aligned} \max_{Q_{:t-1}} p\left(O_{:t}, Q_{:t-1}, q_t = j\right) &= \max_{Q_{:t-1}} \left( p\left(O_{:t-1}, Q_{:t-1}, q_t = j\right) \cdot p\left(o_t \mid q_t = j\right) \right)\\ &= \max_{Q_{:t-2},i} \left( p\left(O_{:t-1}, Q_{:t-2}, q_{t-1} = i, q_t = j\right)\cdot p\left(o_t \mid q_t = j\right) \right)\\ &= \max_{Q_{:t-2},i} \left( p\left(O_{:t-1}, Q_{:t-2}, q_{t-1} = i\right)\cdot p\left(q_t = j \mid q_{t-1} = i\right)\cdot p\left(o_t \mid q_t = j\right) \right)\\ &=\max_i \left( \max_{Q_{:t-2}} p\left(O_{:t-1}, Q_{:t-2}, q_{t-1} = i\right) \cdot p\left(q_t = j \mid q_{t-1} = i\right) \cdot p\left(o_t \mid q_t = j\right) \right) \end{aligned} \] 同样引入 \(\delta\left(t, j\right) = \displaystyle\max_{Q_{:t-1}} p\left(O_{:t}, Q_{:t-1}, q_t = j\right)\) 来简化表示,我们得到 \[ \begin{cases} \displaystyle\delta\left(t, j\right)=b_j\left(o_t\right) \max_i \left( \delta\left(t-1, i\right)\cdot a_{ij} \right), & t\geq2\\ \displaystyle\delta\left(1, j\right) = \pi\left(j\right) b_j\left(o_1\right),&t=1 \end{cases} \] 又转化为动态规划问题。
Viterbi 的最终结果为 \(\displaystyle\hat{q}_t=\arg\max_{i}\delta\left(t,i\right)\),这些局部的取等条件在动态规划中向后传递,最后变成了整个问题的解。
解决问题的前提: 获取 \(\theta=\{\pi,A,B\}\)
在使用 Viterbi 算法中,我们主要依赖 \(\theta=\{\pi,A=\left(a_{ij}\right),B=\left(b_j\left(o_i\right)\right)\}\) ,这些数据是需要我们先计算的。
监督训练:古典概型
在有标签数据的情况下,我们可以通过计数来估计这些参数:
- 初始状态概率 \(\pi_i\) :
\[ \pi_i = p\left(q_1 = i\right) = \frac{\#\left(q_1 = i\right)}{\# \text{sequences}} \]
- 状态转移概率 \(a_{ij}\) :
\[ a_{ij} = p\left(q_t = j \mid q_{t-1} = i\right) = \frac{\#\left(q_{t-1} = i, q_t = j\right)}{\#\left(q_{t-1} = i, q_t = *\right)} \]
- 发射概率 \(b_i\left(w\right)\) :
\[ b_i\left(w\right) = p\left(o_t = w \mid q_t = i\right) = \frac{\#\left(q_t = i, o_t = w\right)}{\#\left(q_t = i\right)} \]
无监督训练:E-M算法
在无标签或者少量标签数据的情况下,模型参数的优化是通过最大化对数似然函数(需要好好理解为什么!)来完成的。
这里我们以一个样本(就一个句子 \(O=O_1\))为例,目的是讨论算法本身。此时,目标函数为: \[ \log p\left(O\mid \theta\right) = \log \sum_{Q} p\left(O, Q\mid \theta\right) \] 为什么选择最大似然估计?这里给出一个感性的理解:首先,我们认为语言遵循一定的规律,也就是说语言背后有着一个存在的隐式最优模型参数 \(\theta^*\)(当然,随着历史的推移确实可能改变),只要我们选取了大规模的语言样本,让 \(O\) 集合的分布扩散到整个 \(\theta^*\) 的值域,就可以只分析 \(O\) 来拟合 \(\theta^*\)。
- 举例:这就像我们通过训练一些题目来备考高考数学,目的是 generalize 到所有的高考数学问题获取尽可能高的分数,学少了不行,学偏了不行,又没法学太多,因此只能适中选取训练集。
我们有获得大量,某种程度上可以代表 population 到观测样本 \(O\) 后,便可以断言对于所有参数 \(\theta\),只有 \(\theta=\theta^*\) 才会使得 \(p\left(O\mid \theta\right)\) 最大,不然更优的 \(\theta^\prime\) 应当被认为是更好的参数:\(\theta^\prime\) 相比 \(\theta^*\) 使得模型生成了更大比例的“语言”。
注:这是是一种优化方案,不是唯一,其他方案也可能是可行的,上面的描述也只是the description of intuition.
E-M 算法的步骤如下:
使用 Jensen 不等式来处理对数似然函数,其中 \(q\left(\cdot\right)\) 是一个待定的权重: \[ \begin{aligned} \log p\left(O\mid \theta\right) &= \log \sum_{Q} p\left(O, Q\mid \theta\right) = \log \sum_{Q} \left( q\left(Q\right) \frac{p\left(O, Q\mid \theta\right)}{q\left(Q\right)} \right)\\ & \geq \sum_{Q} q\left(Q\right) \log\left(\frac{p\left(O, Q\mid \theta\right)}{q\left(Q\right)} \right)\\ & =\sum_Q q\left(Q\right) \log p\left(O, Q\mid \theta\right) + \text{entropy}\left(q\left(Q\right)\right) \end{aligned} \]
处理待定的权重函数 \(q\) :
如果 \(q\) 已经被给定,则熵项为常数,我们定义 \(Q-\) 函数为 \[ S=\sum_{Q}q\left(Q\right)\log p\left(O,Q\mid \theta\right) \] 在第 \(k\) 次迭代中,令 \(q\left(Q\right) = p\left(Q\mid O,\theta_k\right)\),目标是最大化此次迭代中的 \(S\),记带入这个 \(q\) 的 \(S\) 为 \(Q\left(\theta\mid \theta_k\right)\)。
为什么选取这个 \(Q-\) 函数?这是因为 \[ \begin{aligned} \log p\left(O\mid \theta\right) &=\log p\left(O\mid \theta\right) \sum_Q q\left(Q\right) = \sum_Q q\left(Q\right) \log p\left(O\mid \theta\right)\\ &=\sum_Q q\left(Q\right) \left[ \log \frac{p\left(O, Q\mid \theta\right)}{p\left(Q\mid O, \theta\right)} \right]\\ &=\sum_Q q\left(Q\right) \log p\left(O, Q\mid \theta\right) - \sum_Q q\left(Q\right) \log p\left(Q\mid O, \theta\right)\\ &=\sum_Q q\left(Q\right) \log p\left(O, Q\mid \theta\right) - \sum_Q q\left(Q\right) \log p\left(Q\mid O, \theta\right) \\ &\phantom{\sum\sum\sum}+ \sum_Q q\left(Q\right) \log q\left(Q\right) - \sum_Q q\left(Q\right) \log q\left(Q\right)\\ &=\sum_Q q\left(Q\right) \log p\left(O, Q\mid \theta\right) +\text{entropy}\left(q\left(Q\right)\right) + \left[ \sum_Q q\left(Q\right) \log \frac{q\left(Q\right)}{\log p\left(Q\mid O, \theta\right)} \right]\\ &=\sum_Q q\left(Q\right) \log p\left(O, Q\mid \theta\right) + KL\left(q\left(Q\right) \parallel p\left(Q\mid O, \theta\right)\right) + \text{entropy}\left(q\left(Q\right)\right). \end{aligned} \] 如果令 \(q\left(Q\right) = p\left(Q\mid O,\theta_k\right)\) ,此时的 \(Q\) 函数可以看作是 \(\log p\left(O\mid \theta\right)\) 的局部近似:其中的 KL 散度项随着 \(\theta\) 逐步接近 \(\theta_k\) 而缩小,因此可以忽略。
注:KL 散度是 \[ \begin{aligned} KL\left(p\left(x\right)\parallel q\left(x\right)\right)&=\sum_{x\in\Omega}p\left(x\right)\log p\left(x\right)-\sum_{x\in\Omega}p\left(x\right)\log q\left(x\right)\\ &=\sum_{x\in\Omega}p\left(x\right)\log \frac{p\left(x\right)}{q\left(x\right)}\\ &=-\sum_{x\in\Omega}p\left(x\right)\log \frac{q\left(x\right)}{p\left(x\right)}\\ &\geq-\sum_{x\in\Omega}p\left(x\right)\left(\frac{q\left(x\right)}{p\left(x\right)}-1\right)=0 \end{aligned} \] 取等条件当且仅当 \(p\left(\cdot\right)=q\left(\cdot\right)\) .
- 回到优化 \(S\),我们有
\[ \begin{aligned} Q\left(\theta\mid \theta_k\right) &= \sum_Q p\left(Q\mid O, \theta_k\right) \log p\left(O, Q\mid \theta\right)\\ &=\sum_Q p\left(Q\mid O, \theta_k\right) \log \left(\prod_{t=1}^{T} a_{q_{t-1}q_t}\, b_{q_t}\left(o_t\right)\right)\\ &=\sum_{t, i, j} p\left(Q_{t-1} = i, Q_t = j \mid O, \theta_k\right) \log a_{ij} + \sum_{t, j} p\left(Q_t = j \mid O, \theta_k\right) \log b_j\left(o_t\right) \end{aligned} \]
我们解得此条件下最优的 \(a_{ij}\) 为 \[ \hat{a}_{ij} = \frac{\displaystyle\sum_{t, o} p\left(Q_{t-1} = i, Q_t = j, O\mid \theta_k\right)}{\displaystyle\sum_{t, o, *} p\left(Q_{t-1} = i, Q_t = *, O\mid \theta_k\right)} \] 以及最优的 \(b_i\left(o_t\right)\) 为 \[ \hat{b}_i\left(w\right) = \frac{\displaystyle\sum_{t} p\left(Q_t = i, o_t=w \mid O, \theta_k\right)}{\displaystyle\sum_{t,*} p\left(Q_t = i, o_t=* \mid O, \theta_k\right)} \]