ML Lecture 1-4
我们将研究多元函数 \(f\left(\mathbf x\right):\mathbb R^n\to \mathbb R\) 上的最优化问题。假设 \(f\) 二阶可导。
梯度下降
凸函数
若 \(f\left(\mathbf x\right)\) 满足 Jensen 不等式 \[ f\left(k\mathbf x_1+\left(1-k\right)\mathbf x_2\right)\leq k f\left(\mathbf x_1\right)+\left(1-k\right)f\left(\mathbf x_2\right) \] 称 \(f\left(\mathbf x\right)\) 是凸的。
在 \(\mathbf x\) 处取方向向量 \(\mathbf e\),对应的方向二阶导数是 \(\mathbf e^TH\mathbf e\),其中 \(H\) 是海赛矩阵。由凸性,方向二阶导数非负,故海赛矩阵半正定。
函数的光滑性
对于 \(L\in\mathbb R\),若 \(f\left(\mathbf x\right)\) 满足梯度 \(\nabla f\) 是 \(L\)-continuous 的,即 \[ \Vert \nabla f\left(\mathbf x_1\right)-\nabla f\left(\mathbf x_2\right)\Vert\leq L\Vert \mathbf x_1-\mathbf x_2\Vert \] 称 \(f\) 是 \(L\)-smooth 的。
记 \(\mathbf g\left(\mathbf x\right)=\nabla f\left(\mathbf x\right)\),则 \(\nabla \mathbf g\) 就是 \(f\) 的海赛矩阵。记海赛矩阵为 \(H\),方向导数是 \(H\mathbf e\)。
选择 \(\mathbf x_1\) 和 \(\mathbf x_2\) 之间的直线进行积分,\(\mathbf g\left(\mathbf x_1\right)-\mathbf g\left(\mathbf x_2\right)\) 是方向导数的积分。可知方向导数的模长 \(\leq L\),即海赛矩阵 \(H\) 满足 \(\Vert H\Vert\leq L\)。
光滑函数的二次上界
\(f\left(\mathbf x\right)\) 是 \(L\)-smooth 的,则它在 \(\mathbf x_0\) 处有二次上界 \[ f\left(\mathbf x\right)\leq f\left(\mathbf x_0\right)+\langle\nabla f\left(\mathbf x_0\right),\mathbf x-\mathbf x_0\rangle + \dfrac{L}{2}\Vert \mathbf x-\mathbf x_0\Vert^2 \] 证明:记 \[ g\left(\mathbf x\right)=f\left(\mathbf x_0\right)+\langle\nabla f\left(\mathbf x_0\right),\mathbf x-\mathbf x_0\rangle+\dfrac{L}{2}\Vert \mathbf x-\mathbf x_0\Vert^2 - f\left(\mathbf x\right) \] 则 \(g\left(\mathbf x_0\right)=0\),\(\nabla g\left(\mathbf x_0\right)=\mathbf 0\),海赛矩阵半正定。故 \(g\) 是凸函数,且 \(g\left(\mathbf x_0\right)\) 是最小值。
光滑函数上梯度下降的单调性
对于 \(L-\)smooth 的 \(f\left(x\right)\),观察 \[ f\left(\mathbf x\right)\leq f\left(\mathbf x_0\right)+\langle\nabla f\left(\mathbf x_0\right),\mathbf x-\mathbf x_0\rangle + \dfrac{L}{2}\Vert \mathbf x-\mathbf x_0\Vert^2 \] 记学习率为 \(\eta\),令 \(\mathbf x=\mathbf x_0-\eta\nabla f\left(\mathbf x_0\right)\),则 \[ f\left(\mathbf x_0-\eta\nabla f\left(\mathbf x_0\right)\right)\leq f\left(\mathbf x_0\right)-\eta\Vert\nabla f\left(\mathbf x_0\right)\Vert^2 +\dfrac{L\eta^2}{2}\Vert \mathbf \nabla f\left(\mathbf x_0\right)\Vert^2 \] 令 \(\eta\leq \frac{1}{L}\),则 \[ f\left(\mathbf x_0-\eta\nabla f\left(\mathbf x_0\right)\right)\leq f\left(\mathbf x_0\right)-\frac{\eta}{2}\Vert\nabla f\left(\mathbf x_0\right)\Vert^2 \] 这说明:选择足够小的 \(\eta\),光滑函数上梯度下降一定使得函数值更小。
凸函数上梯度下降的收敛性
\(f\left(\mathbf x\right)\) 是凸的,且是 \(L\)-smooth 的,设 \(f\left(\mathbf x\right)\) 的最小值是 \(f^*=f\left(\mathbf x^*\right)\),从 \(\mathbf x_0\) 出发,进行梯度下降。记 \[ \mathbf x_{t+1}=\mathbf x_t-\eta\nabla f\left(\mathbf x_t\right). \] 其中 \(\eta\leq \frac{1}{L}\)。
有以下收敛性质 \[ f\left(\mathbf x_t\right)-f^*\leq \dfrac{\Vert\mathbf x_0-\mathbf x^*\Vert^2}{2t\mu} \] 这说明误差是 \(O\left(1/t\right)\)。换句话说,如果需要达到 \(\epsilon\) 的精度,只需迭代 \(O\left(1/\epsilon\right)\) 次。
证明:我们希望比较 \(f\left(\mathbf x_{t+1}\right)\) 和 \(f^*\)。 \[ \begin{aligned} f\left(\mathbf x_{t+1}\right)&\leq f\left(\mathbf x_t\right)-\frac{\eta}{2}\Vert\nabla f\left(\mathbf x_t\right)\Vert^2&\left(\text{光滑函数上的梯度下降}\right)\\ &\leq f\left(\mathbf x^*\right)+\langle\nabla f\left(\mathbf x_t\right),\mathbf x_t-\mathbf x^*\rangle-\frac{\eta}{2}\Vert\nabla f\left(\mathbf x_t\right)\Vert^2&\left(\text{凸函数的性质}\right)\\ f\left(\mathbf x_{t+1}\right)-f\left(\mathbf x^*\right)&\leq \dfrac{1}{2\eta}\left(\Vert \mathbf x_t-\mathbf x^*\Vert^2-\Vert \mathbf x_t-\mathbf x^*-\eta\nabla f\left(\mathbf x_t\right)\Vert^2\right)&\left(\text{配方}\right)\\ &=\dfrac{1}{2\eta}\left(\Vert \mathbf x_t-\mathbf x^*\Vert^2-\Vert\mathbf x_{t+1}-\mathbf x^*\Vert^2\right)&\left(\text{递推定义}\right) \end{aligned} \] 将它们求和,错位相消 \[ \sum_{k=1}^t\left(f\left(\mathbf x_k\right)-f\left(\mathbf x^*\right)\right)\leq \dfrac{1}{2\eta} \Vert \mathbf x_0-\mathbf x^*\Vert^2 \] 又因为 \(f\left(\mathbf x_t\right)-f\left(\mathbf x^*\right)\) 是求和中最小的,故 \[ f\left(\mathbf x_t\right)-f\left(\mathbf x^*\right)\leq \dfrac{1}{2t\eta}\Vert \mathbf x_0-\mathbf x^*\Vert^2 \]
强凸函数
若 \(f\left(\mathbf x\right)\) 的海赛矩阵 \(H\) 满足特征值 \(\geq \mu\)(\(\mu>0\)),称 \(f\left(\mathbf x\right)\) 是 \(\mu\)-strongly convex 的。
强凸函数的二次下界
\(f\left(\mathbf x\right)\) 是 \(\mu\)-strongly convex 的,则它在 \(\mathbf x_0\) 处有二次下界 \[ f\left(\mathbf x\right)\geq f\left(\mathbf x_0\right)+\langle\nabla f\left(\mathbf x_0\right),\mathbf x-\mathbf x_0\rangle + \dfrac{\mu}{2}\Vert \mathbf x-\mathbf x_0\Vert^2 \] 证明:记 \[ g\left(\mathbf x\right)=f\left(\mathbf x\right)-\left(f\left(\mathbf x_0\right)+\langle\nabla f\left(\mathbf x_0\right),\mathbf x-\mathbf x_0\rangle+\dfrac{\mu}{2}\Vert \mathbf x-\mathbf x_0\Vert^2\right) \] 则 \(g\left(\mathbf x_0\right)=0\),\(\nabla g\left(\mathbf x_0\right)=\mathbf 0\),海赛矩阵正定。故 \(g\) 是凸函数,且 \(g\left(\mathbf x_0\right)\) 是最小值。
强凸函数上的梯度下降
\(f\left(\mathbf x\right)\) \(\mu\)-strongly convex 且 \(L\)-smooth,设 \(f\left(\mathbf x\right)\) 的最小值是 \(f^*=f\left(\mathbf x^*\right)\)。
- 定界
从最小值点出发,\(f\) 的“陡峭程度变化率”有下界 \(\mu\) 和上界 \(L\),这会带来许多有用的性质。
对于 \(\mathbf x\),称 \(f\left(\mathbf x\right)-f^*\) 为它的"高度",\(\Vert\mathbf x-\mathbf x^*\Vert\) 是它的"距离",\(\Vert \nabla f\left(\mathbf x\right)\Vert\) 是它的 \(\Vert \nabla f\Vert\) ,强凸性可以将这三者统一起来。
在 \(\mathbf x^*\) 处应用 \(f\) 的二次上下界,注意到 \(\nabla f\left(\mathbf x^*\right)=\mathbf 0\): \[ \dfrac{\mu}{2}\Vert \mathbf x^*-\mathbf x\Vert^2\leq f\left(\mathbf x\right)-f^*\leq\dfrac{L}{2}\Vert \mathbf x^*-\mathbf x\Vert^2 \] 这说明高度和距离的平方线性相关。
此外,对 \(f\) 的二次上下界 \[ f\left(\mathbf x_0\right)+\langle\nabla f\left(\mathbf x_0\right),\mathbf x-\mathbf x_0\rangle + \dfrac{\mu}{2}\Vert \mathbf x-\mathbf x_0\Vert^2\\\leq f\left(\mathbf x\right)\leq\\ f\left(\mathbf x_0\right)+\langle\nabla f\left(\mathbf x_0\right),\mathbf x-\mathbf x_0\rangle + \dfrac{L}{2}\Vert \mathbf x-\mathbf x_0\Vert^2 \] 三部分同取最小值(在左右侧,必使 \(f\left(\mathbf x_0\right),\mathbf x-\mathbf x_0\) 反向,此时是 \(\Vert \mathbf x-\mathbf x_0\Vert\) 的二次函数),得 \[ f\left(\mathbf x_0\right)-\frac{1}{2\mu}\Vert f\left(\mathbf x_0\right)\Vert^2\leq f^*\leq f\left(\mathbf x_0\right)-\frac{1}{2L}\Vert f\left(\mathbf x_0\right)\Vert^2 \] 即 \[ \frac{1}{2L}\Vert\nabla f\left(\mathbf x\right)\Vert^2\leq f\left(\mathbf x\right)-f^*\leq \frac{1}{2\mu}\Vert\nabla f\left(\mathbf x\right)\Vert^2 \] 这说明高度和 \(\Vert\nabla f\Vert^2\) 线性相关。
- 梯度下降
根据前文的讨论,若认为 \(\mu,L\) 都是常数,我们可以在 \(f\left(\mathbf x\right)-f^*,\Vert \mathbf x-\mathbf x^*\Vert^2,\Vert\nabla f\left(\mathbf x\right)\Vert^2\leq\epsilon\) 中三者任取其一进行分析,最终都能得到同阶的结果。
取 \(\eta\leq \frac{1}{L}\) 进行梯度下降,构造递推 \(\mathbf x_{t+1}=\mathbf x_t-\eta\nabla f\left(\mathbf x_t\right)\) \[ \begin{aligned} f\left(\mathbf x_{t+1}\right)&\leq f\left(\mathbf x_t\right)-\frac{\eta}{2}\Vert\nabla f\left(\mathbf x_t\right)\Vert^2&\left(\text{光滑函数上的梯度下降}\right)\\ &\leq f\left(\mathbf x_t\right)-\eta\mu\left(f\left(\mathbf x_t\right)-f^*\right)&\left(\text{差值和}\Vert\nabla f\Vert\text{的关系}\right)\\ f\left(\mathbf x_{t+1}\right)-f^*&\leq\left(1-\eta\mu\right)\left(f\left(\mathbf x_t\right)-f^*\right) \end{aligned} \] 可知 \[ f\left(\mathbf x_t\right)-f^*\leq\left(1-\eta\mu\right)^t\left(f\left(\mathbf x_0\right)-f^*\right) \] 高度是指数下降的。要达到 \(\epsilon\) 的精度只需要 \(\displaystyle O\left(\log\frac{1}{\epsilon}\right)\) 步,即强凸函数上的梯度下降是线性收敛(linear convergence)的。
非凸函数上梯度下降的收敛性
对于非凸函数,梯度下降无法保证得到最小值,但可以得到驻点(stationary point),即 \(\nabla f=0\) 的点,包括局部极小值、局部极大值、鞍点。
\(f\left(\mathbf x\right)\) 是 \(L\)-smooth 的,我们希望得到近似驻点,即 \(\mathbf x^{\circ}\) 满足 \(\Vert\nabla f\left(\mathbf x^{\circ}\right)\Vert\leq \epsilon\)。
取 \(\eta\leq \frac{1}{L}\) 进行梯度下降,有以下收敛性质 \[ \min_{k=1}^t\Vert \nabla f\left(\mathbf x_k\right)\Vert^2\leq \dfrac{2\left(f\left(\mathbf x_0\right)-f^*\right)}{\eta t} \] 目标是 \(O\left(1/t\right)\leq \epsilon^2\),迭代次数 \(t=O\left(1/\epsilon^2\right)\)。
证明:将 \(f\left(\mathbf x_{t+1}\right)\leq f\left(\mathbf x_t\right)-\frac{\eta}{2}\Vert\nabla f\left(\mathbf x_t\right)\Vert^2\) 求和得 \[ \begin{aligned} f\left(\mathbf x_t\right)&\leq f\left(\mathbf x_0\right)-\frac{\eta}{2}\sum_{k=0}^{t-1}\Vert\nabla f\left(\mathbf x_k\right)\Vert^2\\ \frac{\eta}{2}\sum_{k=0}^{t-1}\Vert\nabla f\left(\mathbf x_k\right)\Vert^2&\leq f\left(\mathbf x_0\right)-f\left(\mathbf x_t\right)\leq f\left(\mathbf x_0\right)-f^* \end{aligned} \] 在求和中取最小值,得 \[ \min_{k=1}^t\Vert \nabla f\left(\mathbf x_k\right)\Vert^2\leq \dfrac{2\left(f\left(\mathbf x_0\right)-f^*\right)}{\mu t} \]
阶段总结
光滑性规定了海赛矩阵特征值的上界,凸性规定了海赛矩阵特征值的下界,它们反映在函数的二次上下界的二次项系数上。
三种情形的收敛性如下:
| \(f\) 的性质 | 目标 | 所需迭代次数 |
|---|---|---|
| 非凸 | \(\Vert\nabla f\left(\mathbf x\right)\Vert\leq\epsilon\) | \(O\left(1/\epsilon^2\right)\) |
| 凸 | \(f\left(\mathbf x\right)-f^*\leq\epsilon\) | \(O\left(1/\epsilon\right)\) |
| 强凸 | \(f\left(\mathbf x\right)-f^*,\Vert \mathbf x-\mathbf x^*\Vert,\Vert\nabla f\left(\mathbf x\right)\Vert\leq\epsilon\) | \(O\left(\log\frac{1}{\epsilon}\right)\) |
随机梯度下降
我们可能使用近似算法来计算梯度,这会产生误差,假设误差的期望为 \(\mathbf 0\)(我们得到的是无偏估计),方差为 \(\sigma^2\)(每一维方差的和)。
光滑函数上随机梯度下降的近似单调性
\(f\left(\mathbf x\right)\) 是 \(L\)-smooth 的,设 \(f\left(\mathbf x\right)\) 的最小值是 \(f^*=f\left(\mathbf x^*\right)\),从 \(\mathbf x_0\) 出发,进行随机梯度下降。记 \[ \mathbf x^+=\mathbf x-\eta\left(\nabla f\left(\mathbf x\right)+\xi\right). \] 其中 \(\xi\) 是噪声,\(\eta\leq \frac{1}{L}\)。
记 \(\mathbf g=\nabla f\left(\mathbf x\right)+\xi\),则 \[ \begin{aligned} \mathrm E\,\mathbf g&=\nabla f\left(\mathbf x\right)\\ \sigma^2=\mathrm{Var}\,\mathbf g&=\mathrm E\,\Vert \mathbf g\Vert^2-\Vert\mathrm E\,\mathbf g\Vert^2=\mathrm E\Vert \mathbf g\Vert^2-\Vert \nabla f\left(\mathbf x\right)\Vert^2 \end{aligned} \]
\[ \begin{aligned} \mathrm Ef\left(\mathbf x^{+}\right)&\leq \mathrm E\left(f\left(\mathbf x\right)+\langle\nabla f\left(\mathbf x\right),\mathbf x^{+}-\mathbf x\rangle + \dfrac{L}{2}\Vert \mathbf x^{+}-\mathbf x\Vert^2\right)&\text{(光滑函数的二次上界)}\\ &=f\left(\mathbf x\right)-\eta\,\langle\nabla f\left(\mathbf x\right),\mathrm E\,\mathbf g\rangle + \dfrac{L\eta^2}{2}\mathrm E\,\Vert \mathbf g\Vert^2&\text{(期望的线性性)}\\ &=f\left(\mathbf x\right)-\eta\,\Vert\nabla f\left(\mathbf x\right)\Vert^2+ \dfrac{L\eta^2}{2}\left(\Vert \nabla f\left(\mathbf x\right)\Vert^2+\sigma^2\right)&(\mathbf g\,\text{无偏,方差公式)}\\ &\leq f\left(\mathbf x\right)-\frac{\eta}{2}\Vert\nabla f\left(\mathbf x\right)\Vert^2+\frac{\eta}{2}\sigma^2&\left(\eta\leq\tfrac{1}{L}\right)\\ \end{aligned} \]
随机梯度下降基本使得函数值更小,误差不超过 \(\frac{\eta}{2}\sigma^2\)。
凸函数上随机梯度下降的收敛性
\(f\left(\mathbf x\right)\) 是凸的,且是 \(L\)-smooth 的,设 \(f\left(\mathbf x\right)\) 的最小值是 \(f^*=f\left(\mathbf x^*\right)\),从 \(\mathbf x_0\) 出发,进行随机梯度下降。记 \[ \mathbf x_{t+1}=\mathbf x_t-\eta\left(\nabla f\left(\mathbf x_t\right)+\xi_t\right). \] 其中 \(\xi_t\) 是噪声,\(\eta\leq \frac{1}{L}\)。
有以下收敛性质 \[ \mathrm Ef\left(\overline{\mathbf x_t}\right)-f^*\leq \dfrac{\Vert\mathbf x_0-\mathbf x^*\Vert^2}{2t\eta}+\eta\sigma^2 \] 其中 \(\displaystyle\overline{\mathbf x_t}=\frac{1}{t}\sum_{k=1}^t\mathbf x_k\)。
如果需要达到 \(\epsilon\) 的精度,需要取 \(\displaystyle\eta=O\left(\frac{\epsilon}{\sigma^2}\right)\)(假设 \(\eta\leq \frac{1}{L}\)),迭代次数 \(O\left(1/\epsilon^2\right)\)。
证明:记 \(\mathbf g_t=\nabla f\left(\mathbf x_t\right)+\xi_t\) \[ \begin{aligned} \mathrm Ef\left(\mathbf x_{t+1}\right)&\leq f\left(\mathbf x_t\right)-\frac{\eta}{2}\Vert\nabla f\left(\mathbf x_t\right)\Vert^2+\frac{\eta}{2}\sigma^2&\left(\text{光滑函数上的随机梯度下降}\right)\\ &\leq f\left(\mathbf x^*\right)+\langle\nabla f\left(\mathbf x_t\right),\mathbf x_t-\mathbf x^*\rangle-\frac{\eta}{2}\Vert\nabla f\left(\mathbf x_t\right)\Vert^2+\frac{\eta}{2}\sigma^2&\left(\text{凸函数的性质}\right)\\ \mathrm Ef\left(\mathbf x_{t+1}\right)-f\left(\mathbf x^*\right)&\leq\mathrm E\,\langle\mathbf g_t,\mathbf x_t-\mathbf x^*\rangle-\frac{\eta}{2}\mathrm E\Vert\mathbf g_t\Vert^2+\eta\sigma^2&\left(\text{表示成}\,\mathbf g_t\,\text{的期望}\right)\\ &\leq\mathrm E\left(\Vert \mathbf x_t-\mathbf x^*\Vert^2-\Vert\mathbf x_{t+1}-\mathbf x^*\Vert^2\right)+\eta\sigma^2&\left(\text{期望的线性性,配方,递推定义}\right)\\ \end{aligned} \]
将差值求和,和之前类似,只是多了误差项 \(t\eta\sigma^2\)。 \[ \sum_{k=1}^t\left(\mathrm Ef\left(\mathbf x_k\right)-f\left(\mathbf x^*\right)\right)\leq \dfrac{1}{2\eta} \Vert \mathbf x_0-\mathbf x^*\Vert^2+t\eta\sigma^2 \] \(f\) 是凸的,根据 Jensen 不等式 \[ \mathrm E f\left(\overline{\mathbf x_t}\right)\leq\frac{1}{t}\sum_{k=1}^t\mathrm Ef\left(\mathbf x_k\right)=f^*+\dfrac{1}{2t\eta} \Vert \mathbf x_0-\mathbf x^*\Vert^2+\eta\sigma^2 \]
强凸函数上随机梯度下降的收敛性
\(f\left(\mathbf x\right)\) \(\mu\)-strong convex 且 \(L\)-smooth,进行随机梯度下降。
套用凸函数的结论 \[ \mathrm Ef\left(\overline{\mathbf x_t}\right)-f^*\leq \dfrac{\Vert\mathbf x_0-\mathbf x^*\Vert^2}{2t\eta}+\eta\sigma^2 \] 用强凸函数的性质将距离转为高度 \[ \mathrm Ef\left(\overline{\mathbf x_t}\right)-f^* \leq \frac{1}{t\mu\eta}\left(f\left(\mathbf x_0\right)-f^*\right)+\eta\sigma^2 \] 考虑每 \(m\) 次为一轮,令 \(\displaystyle m>\frac{1}{\mu\eta}\),则系数 \(\displaystyle \frac{1}{m\mu\eta}<1\),记 \(\displaystyle c=\frac{1}{m\mu\eta}\)。
记数列 \(\{D_n\}\) 满足 \(D_0=f\left(\mathbf x_0\right)-f^*\),\(D_{n+1}=cD_n+\eta\sigma^2\),\(D_n\) 描述了第 \(n\) 轮完成后,期望高度的上界。 \[ \begin{aligned} D_{n+1}-\frac{\eta\sigma^2}{1-c}&=c\left(D_n-\frac{\eta\sigma^2}{1-c}\right)\\ D_n&=c^nD_0+\left(1-c^n\right)\frac{\eta\sigma^2}{1-c}\\ &=c^nD_0+O\left(\eta\sigma^2\right) \end{aligned} \] 为了达到 \(\epsilon\) 的精度,需要令 \(\displaystyle \eta=O\left(\epsilon\right)\),轮数为 \(\displaystyle O\left(\log\frac{1}{\epsilon}\right)\),每轮迭代 \(\displaystyle m=O\left(\frac{1}{\epsilon}\right)\) 次,总迭代次数为 \(\displaystyle O\left(\frac{1}{\epsilon}\log\frac{1}{\epsilon}\right)\)。
可以进一步证到 \(\displaystyle O\left(\frac{1}{\epsilon}\right)\),见文献 "Lacoste-Julien S, Schmidt M, Bach F. A simpler approach to obtaining an \(o\left(1/t\right)\) convergence rate for projected stochastic subgradient descent. arXiv preprint arXiv:1212.2002, 2012."
随机梯度下降的具体描述
让我们更细致的描述随机梯度下降的过程:
假设有 \(n\) 个数据,第 \(i\) 个数据的 Loss function 是 \(l_i\left(\mathbf x\right)\),总的 Loss function \(f\left(\mathbf x\right)\) 是 \(n\) 个数据的 Loss function 的均值。 \[ f\left(\mathbf x\right)=\dfrac{1}{n}\sum_{k=1}^nl_i\left(\mathbf x\right) \] 根据 \(\nabla\) 的线性性 \[ \nabla f\left(\mathbf x\right)=\dfrac{1}{n}\sum_{k=1}^n\nabla l_i\left(\mathbf x\right) \] 当我们计算 \(\nabla f\left(\mathbf x\right)\) 时,可以取随机的 \(i\in\{1\sim n\}\),以 \(\nabla l_i\left(\mathbf x\right)\) 作为估计值,这是无偏的(期望相同)。我们假设这么做的方差为 \(\sigma^2\)。
有些算法可能选择 \(\{1\sim n\}\) 的一个子集并求均值,以减小方差,它们的分析是类似的。
SVRG 算法
随机梯度下降之所以难以收敛,主要是方差项 \(\sigma^2\) 的影响。为了取得更快的收敛速度,需要用某种方法削减方差。

设定一个数 \(m\),将每 \(m\) 次迭代称为一轮,记为 \(\mathbf x_{0\sim m}\)。
在每一轮的开始,计算一次精确梯度 \(\nabla f\left(\mathbf x_0\right)\)。这样的开销颇大,但当 \(m\) 较大时可以承受。
当计算到 \(\mathbf x_t\) 时,我们希望计算 \(\nabla f\left(\mathbf x_t\right)\) 的估计值,原先的方法是随机取 \(i\in\{1\sim n\}\),令估计值为 \(\nabla l_i\left(\mathbf x_t\right)\)。
尝试对这个估计进行修正。一个直觉是,\(\mathbf x_t\) 和 \(\mathbf x_0\) 相距不远,\(\nabla f\left(\mathbf x_0\right)\) 与 \(\nabla l_i\left(\mathbf x_0\right)\) 的差值和 \(\nabla f\left(\mathbf x_t\right)\) 与 \(\nabla l_i\left(\mathbf x_t\right)\) 的差值是近似的,于是 \[
\nabla f\left(\mathbf x_t\right)\approx\nabla l_i\left(\mathbf x_t\right)+\nabla f\left(\mathbf x_0\right)-\nabla l_i\left(\mathbf x_0\right)
\] 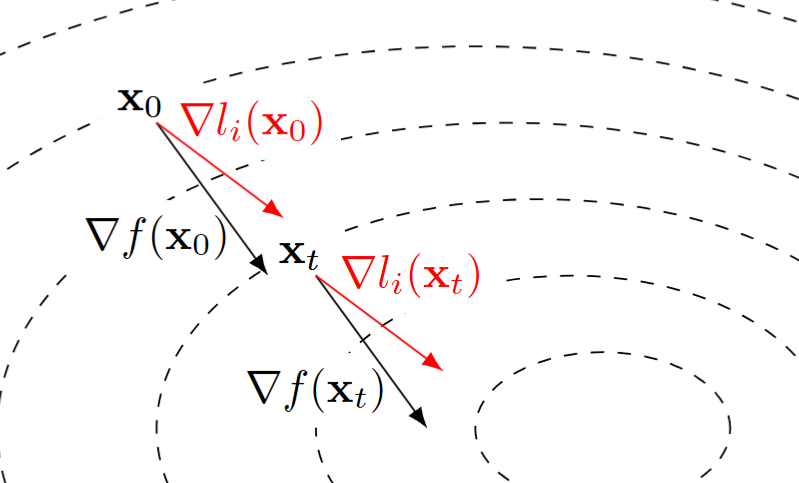
记 \(\mathbf g_t=\nabla l_i\left(\mathbf x_t\right)+\nabla f\left(\mathbf x_0\right)-\nabla l_i\left(\mathbf x_0\right)\),构造递推 \(\mathbf x_{t+1}=\mathbf x_t-\eta \mathbf g_t\)。最终,取 \(\displaystyle\overline{\mathbf x}=\frac{1}{m}\sum_{k=0}^{m-1}\mathbf x_k\) 作为新的结果。
SVRG 的核心思路在于:\(\nabla f\left(\mathbf x_t\right)\) 和 \(\nabla f\left(\mathbf x_0\right)\) 强相关,相比于孤立地估计 \(\nabla f\left(\mathbf x_t\right)\),不如估计它们的差值,那样方差更小。
强凸函数上 SVRG 的收敛性
\(f\left(\mathbf x\right)\) \(\mu\)-strong convex 且 \(L\)-smooth(每个 \(l_i\left(\mathbf x\right)\) 也如此),SVRG 线性收敛。
证明:
模仿凸函数的情形,易得 \[ \sum_{k=0}^{m-1}\left(\mathrm Ef\left(\mathbf x_k\right)-f^*\right)\leq \dfrac{1}{2\eta} \Vert \mathbf x_0-\mathbf x^*\Vert^2+\eta\sum_{k=0}^{m-1}{\rm Var}\,\mathbf g_k \] 我们希望分析 \[ \begin{aligned} {\rm Var}\,\mathbf g_t&={\rm Var}\,\Vert\nabla l_i\left(\mathbf x_t\right)-\nabla l_i\left(\mathbf x_0\right)\Vert\\ &\leq\mathrm E\,\Vert \nabla l_i\left(\mathbf x_t\right)-\nabla l_i\left(\mathbf x_0\right)\Vert^2\\ &\leq2\mathrm E\Vert\nabla l_i\left(\mathbf x_t\right)-\nabla l_i\left(\mathbf x^*\right)\Vert^2+2\mathrm E\Vert \nabla l_i\left(\mathbf x_0\right)-\nabla l_i\left(\mathbf x^*\right)\Vert^2&\left(\Vert a\pm b\Vert^2\leq 2\Vert a\Vert^2+2\Vert b \Vert^2\right)\\ \end{aligned} \]
引理一:\(L\)-smooth 函数 \(h\left(\mathbf x\right)\),满足 \(h\left(\mathbf x\right)\geq 0\) 为最小值,有 \[ \Vert\nabla h\left(\mathbf x\right)\Vert^2\leq 2Lh\left(\mathbf x\right) \] 即:梯度模长增大时,函数值必然随之升高。梯度模长无法瞬变,在变化过程中,一定会积累在函数值上。
证明:从 \(\mathbf x\) 出发,取方向为 \(\nabla h\left(\mathbf x\right)\) 的直线,即 \(h\left(\mathbf x+t\nabla h\left(\mathbf x\right)\right)\)。
在 \(\mathbf x\) 应用光滑函数的二次上界 \[ \begin{matrix} 0\leq h\left(\mathbf x+t\nabla h\left(\mathbf x\right)\right)\leq h\left(\mathbf x\right)+\langle\nabla h\left(\mathbf x\right),t\nabla h\left(\mathbf x\right)\rangle + \dfrac{L}{2}\Vert t\nabla h\left(\mathbf x\right)\Vert^2\\ h\left(\mathbf x\right)+t\Vert\nabla h\left(\mathbf x\right)\Vert^2+\dfrac{L}{2}\Vert\nabla h\left(\mathbf x\right)\Vert^2t^2\geq 0 \end{matrix} \] 取 \(t=-\frac{1}{L}\) 得到最紧的不等式 \[ h\left(\mathbf x\right)-\frac{1}{2L}\Vert\nabla h\left(\mathbf x\right)\Vert^2\geq 0 \]
引理二:\(\mathrm E\Vert\nabla l_i\left(\mathbf x\right)-\nabla l_i\left(\mathbf x^*\right)\Vert^2\leq 2L\left(f\left(\mathbf x\right)-f^*\right)\)。
证明:构造 \(g\left(\mathbf x\right)=l_i\left(\mathbf x\right)-l_i\left(\mathbf x^*\right)-\langle\nabla l_i\left(\mathbf x^*\right),\mathrm x-\mathrm x^*\rangle\),\(\nabla g\left(\mathbf x\right)=\nabla l_i\left(\mathbf x\right)-\nabla l_i\left(\mathbf x^*\right)\)。
\(g\) 是 \(L\)-smooth 且凸的,\(g\) 的最小值是 \(g\left(x^*\right)=0\)。根据引理一,\(\Vert\nabla g\left(\mathbf x\right)\Vert^2\leq 2Lg\left(\mathbf x\right)\),即 \[ \Vert\nabla l_i\left(\mathbf x\right)-\nabla l_i\left(\mathbf x^*\right)\Vert^2\leq 2L\left(l_i\left(\mathbf x\right)-l_i\left(\mathbf x^*\right)-\langle\nabla l_i\left(\mathbf x^*\right),\mathrm x-\mathrm x^*\rangle\right) \] 对全体 \(i\) 求均值,得 \[ \mathrm E\Vert\nabla l_i\left(\mathbf x\right)-\nabla l_i\left(\mathbf x^*\right)\Vert^2\leq 2L\left(f\left(\mathbf x\right)-f\left(\mathbf x^*\right)-\langle\nabla f\left(\mathbf x^*\right),\mathrm x-\mathrm x^*\rangle\right) \] 注意到 \(\nabla f\left(\mathbf x^*\right)=\mathbf 0\) 即证毕。
由引理二,我们有 \[ {\rm Var}\,\mathbf g_t\leq 4L\left(f\left(\mathbf x_t\right)+f\left(\mathbf x_0\right)-2f^*\right) \] 故 \[ \sum_{k=0}^{m-1}\left(\mathrm Ef\left(\mathbf x_k\right)-f^*\right) \leq \dfrac{1}{2\eta} \Vert \mathbf x_0-\mathbf x^*\Vert^2+4\eta L\sum_{k=0}^{m-1}\left(\mathrm Ef\left(\mathbf x_k\right)+f\left(\mathbf x_0\right)-2f^*\right) \] 由强凸性,统一放缩为高度,整理得 \[ \begin{aligned} m\left(1-4\eta L\right)\left(\overline{\mathrm Ef\left(\mathbf x\right)}-f^*\right) &\leq\left(\dfrac{1}{2\eta\mu}+4m\eta L\right)\left(f\left(\mathbf x_0\right)-f^*\right)\\ \left(\overline{\mathrm Ef\left(\mathbf x\right)}-f^*\right) &\leq \left(\dfrac{1}{2m\eta\mu\left(1-4\eta L\right)}+\dfrac{4\eta L}{1-4\eta L}\right)\left(f\left(\mathbf x_0\right)-f^*\right)\\ \end{aligned} \] 再根据 Jensen 不等式,\(\mathrm Ef\left(\overline{\mathbf x}\right) \leq \overline{\mathrm Ef\left(\mathbf x\right)}\)。
当 \(\displaystyle \eta<\frac{1}{8L}\) 且 \(m\) 足够大时,系数 \(<1\),故线性收敛。
当 condition number \(\displaystyle \frac{L}{\mu}\) 较大时,SVRG 比单纯的梯度下降显著更快,因为后者的收敛系数依赖于 condition number,而前者则不然。(梯度下降迭代次数是 \(\displaystyle \frac{L}{\mu}\log\frac{1}{\epsilon}\),而 SVRG 可以做到 \(\displaystyle \log\frac{1}{\epsilon}\),同时每次迭代的开销较少)
Bottou, L., Curtis, F. E., & Nocedal, J. (2018). Optimization Methods for Large-Scale Machine Learning. arXiv. https://arxiv.org/abs/1606.04838↩︎