ML Lecture 5
梯度下降的变种
上一篇文章重点讨论了经典梯度下降在凸函数上的表现,接下来,我们将探讨它的一系列变种。
连续凸函数上的梯度下降
\(f(\mathbf x)\) 凸且 \(\rho\)-Lipschitz,设 \(f(\mathbf x)\) 的最小值是 \(f^*=f(\mathbf x^*)\),从 \(\mathbf x_0\) 出发,进行梯度下降。
注:在 \(L\)-smooth 函数上,只要根据 \(L\) 设置学习率,梯度下降必然单调。在连续(但不光滑)函数上则不然,无论如何设计学习率,梯度下降都可能不单调。
- 梯度下降的步长
\(\rho\)-Lipschitz 表明 \(\Vert\nabla f\Vert\leq\rho\),由 \(\mathbf x_{t+1}=\mathbf x_t-\eta\nabla f(\mathbf x_t)\),知 \(\Vert\mathbf x_{t+1}-\mathbf x_t\Vert^2\leq \eta^2\rho^2\)。
- 收敛性
\[ \begin{aligned} f(\mathbf x_t)-f(\mathbf x^*) &\leq \big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf x^*\big\rangle &\text{(凸性)}\\ &= \frac{1}{\eta}\big\langle\mathbf x_t-\mathbf x_{t+1},\mathbf x_t-\mathbf x^*\big\rangle &\text{(递推定义)}\\ &= \frac{1}{\eta}\Big( \Vert\mathbf x_t\Vert^2 -\langle\mathbf x_t,\mathbf x_{t+1}\rangle -\langle\mathbf x_t,\mathbf x^*\rangle +\langle\mathbf x_{t+1},\mathbf x^*\rangle \Big)\\ &= \frac{1}{2\eta}\Big( \Vert\mathbf x_t-\mathbf x_{t+1}\Vert^2 +\Vert\mathbf x_t-\mathbf x^*\Vert^2 -\Vert\mathbf x_{t+1}-\mathbf x^*\Vert^2 \Big)\\ &\leq \frac{1}{2\eta}\Big( \eta^2\rho^2+ \Vert\mathbf x_t-\mathbf x^*\Vert^2 -\Vert\mathbf x_{t+1}-\mathbf x^*\Vert^2 \Big) &{(\rho\,\text{-Lipschitz})}\\ \end{aligned} \]
对 \(t=0\sim (T-1)\) 求和得 \[ \sum_{t=0}^{T-1}\Big(f(\mathbf x_t)-f^*\Big)\leq\frac{T\eta\rho^2}{2}+\frac{1}{2\eta}\Big(\Vert\mathbf x_0-\mathbf x^*\Vert^2-\Vert\mathbf x_T-\mathbf x^*\Vert^2\Big) \] 设 \(\Vert\mathbf x_0-\mathbf x^*\Vert^2\leq \Theta\),根据 Jensen 不等式 \[ f(\overline{\mathbf x})-f^*\leq \overline{f(\mathbf x_t)}-f^*\leq \frac{\eta\rho^2}{2}+\frac{\Theta}{2\eta T} \] 取 \(\eta=\sqrt{\Theta/\rho^2T}\) 得 \[ f(\overline{\mathbf x})-f^*\leq\frac{\rho\sqrt{\Theta}}{\sqrt{T}} \]
* Projected GD 投影梯度下降
- 带约束的凸优化问题
给出可行集 \(\mathcal X\subset \mathbb R^n\),求 \(\mathbf x\in \mathcal X\) 使得 \(f(\mathbf x)\) 尽量小。其中 \(f\) 是凸的,区域 \(\mathcal X\) 也是凸的。
- 投影梯度下降
面对带约束的优化问题,朴素的 \(\mathbb R^n\) 上的梯度下降不再生效:一步迭代可能让我们离开 \(S\),到达非法区域。
这引出投影梯度下降:先进行梯度下降,然后投影回 \(S\)。
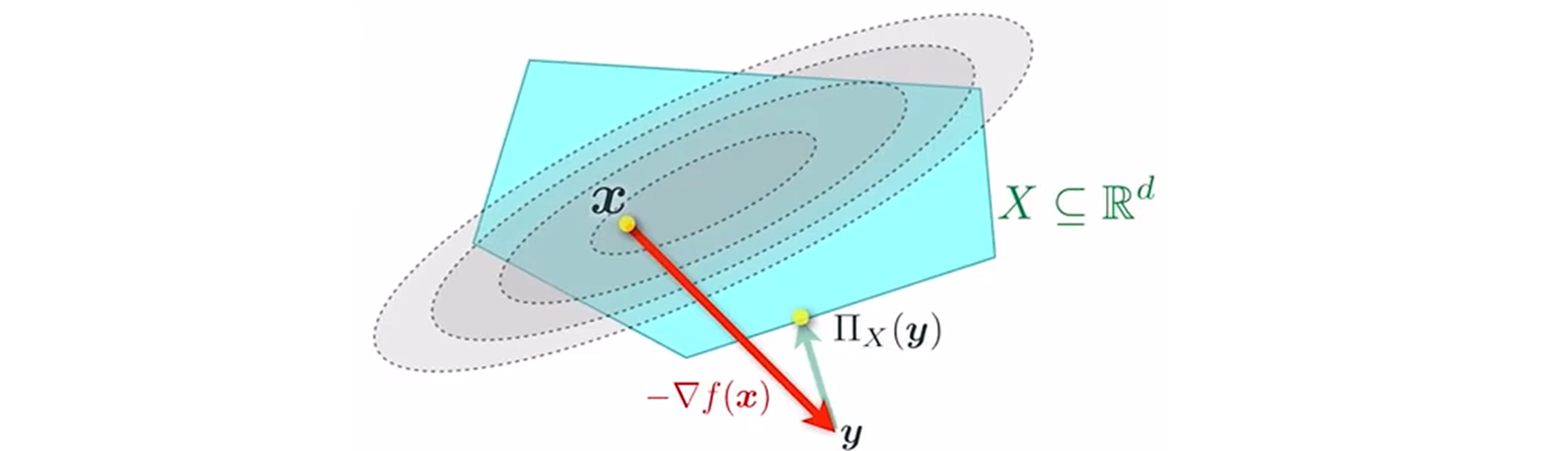
记 \({\rm proj}_S(\mathbf u)={\rm argmin}_{\mathbf x\in S}\Vert \mathbf x-\mathbf u\Vert\),一次迭代可以表示为 \(\mathbf x_{t+1}={\rm proj}_S\big(\mathbf x_t-\eta\nabla f(\mathbf x_{t})\big)\)。
投影梯度下降的收敛性不是本节的重点,略去。
2-范数的局限性
- 投影梯度下降的障碍
对于带约束的优化问题,\(\mathcal X\) 的形状多种多样,基于 2-范数的投影可能难以计算。
我们需要一种易于计算的“投影”,这归根结底是设计合适的“范数”。
- 其他连续性
前文的讨论假定函数 \(f\) 关于 2-范数 \(\rho\)-Lipschitz,如果 \(f\) 关于其他范数 \(\rho\)-Lipschitz 如何呢?
例如 \(f\) 关于 \(\Vert\cdot\Vert_{\infty}\) \(\rho\)-Lipschitz,此时 \(f\) 关于 2-范数 \(\sqrt{n}\rho\)-Lipschitz,沿用 2-范数会使我们携带额外的系数 \(\sqrt{n}\)。我们希望能在分析中直接用 \(\Vert\cdot\Vert_{\infty}\)。
Bregman divergence 贝格曼距离
- 动机
前文提到,有必要用其他范数代替 2-范数,但我们不希望对每种范数都重新作证明。此时,我们希望为所有“良好范数”寻找一种抽象的共同结构,并在这种结构的基础上进行一劳永逸的普适证明。
- 贝格曼距离的定义
对于凸函数 \(w(\mathbf x)\),定义 \(w\) 在 \(\mathbf x\) 处函数值与 \(\mathbf y\) 处一阶近似的差为它们的贝格曼距离 \[ V_{\mathbf y}(\mathbf x)=w(\mathbf x)-w(\mathbf y)-\big\langle\nabla w(\mathbf y),\mathbf x-\mathbf y\big\rangle \] - 贝格曼距离的性质
- \(V_{\mathbf x}(\mathbf x)=0,V_{\mathbf y}(\mathbf x)\geq 0\)。
- 不满足对称性,常有 \(V_{\mathbf y}(\mathbf x)\neq V_{\mathbf x}(\mathbf y)\)。
- 给定 \(\mathbf y\) 后 \(V_{\mathbf y}(\mathbf x)\) 是凸的。
- 当 \(w(\mathbf x)\) \(\mu\)-strongly convex 时,\(V_{\mathbf y}(\mathbf x)\geq\frac{\mu}{2}\Vert \mathbf x-\mathbf y\Vert\)。
- 如果将 \(V\) 看做施加在 \(w\) 上的算符,则 \(V\) 具有线性性:\(V_{\alpha w_1+\beta w_2}=\alpha V_{w_1}+\beta V_{w_2}\)。
- 对于点 \(\mathbf x_{1\sim n}\),\(\sum_{k=1}^nV_{\mathbf y}(\mathbf x_k)\geq \sum_{k=1}^nV_{\overline{\mathbf x}}(\mathbf x_k)\)。
Bergman Divergence 有一个非常重要的梯度下降形式: \[ \begin{aligned} \left \langle \nabla V_x(y),y-u \right \rangle &= \left \langle \nabla w(y)-w(x),y-u \right \rangle\\ &= \left \langle \nabla w(y),y-u \right \rangle - \left \langle \nabla w(x),y-u \right \rangle\\ &= \left \langle \nabla w(y),y-u \right \rangle - \left \langle \nabla w(x),y-x \right \rangle - \left \langle \nabla w(x),x-u \right \rangle\\ &=-\left (w(u)-w(y) -V_y(u) \right )-\left (w(y)-w(x) -V_x(y) \right )\\ & \phantom{=-\left (w(u)-w(y) -V_y(u) \right )\ }+\left (w(u)-w(x) -V_x(u) \right )\\ &=\big[V_x(y)-V_x(u)\big]+V_y(u) \end{aligned} \] - 为啥考虑贝格曼距离?
贝格曼距离是“良好范数”的抽象总括。
注意最后一项性质,它指出,如果我们有一些点 \(\mathbf x_{1\sim n}\),希望选出一个点 \(\mathbf y\) 到它们的距离和最小,则 \(\mathbf y\) 一定在 \(\mathbf x_{1\sim n}\) 的平均值处。这是“距离函数”所需的一项重要性质,又可以证明,贝格曼距离穷尽了所有符合该性质的函数。
Proof: \[ \frac{1}{n}\left(\sum_{k=1}^nV_{\mathbf y}(\mathbf x_k)-\sum_{k=1}^nV_{\overline{\mathbf x}}(\mathbf x_k)\right)=w(\overline{\mathbf x})-w(\mathbf y)-\langle\nabla f(\mathbf y),\overline{\mathbf x}-\mathbf y\rangle=V_{\mathbf y}(\overline{\mathbf x})\geq 0. \]
欧式距离、KL-散度、马氏距离等都是 Bregman divergence 的一种特例。
Mirror Descent 镜像梯度下降
接下来,我们将从两种视角解释镜像梯度下降,它是梯度下降在贝格曼距离上的扩展版本。
- 视角一:正则化
回顾梯度下降的基本思想:在 \(\mathbf x_t\) 处求线性拟合,\(-\nabla f(\mathbf x_t)\) 的方向就是函数值下降最快的方向,于是沿其前进 \(\eta\)。然而,由于 \(L\)-smooth 的限制, \(\eta\) 并非越大越好,当 \(\eta\) 足够小时,才能保证每一步都会使函数值减小。上一篇文章验证了 \(\eta=\frac{1}{L}\) 是合适的,下面我们解释它的来源。
我们知道 \(f\) 是 \(L\)-smooth 的,在 \(\mathbf x_t\) 附近,线性拟合效果不错,但在远处效果较差。一个直觉是:不能让迭代结果离 \(\mathbf x_t\) 太远,为此,增加正则化项 \(\Vert\mathbf x-\mathbf x_t\mathbf\Vert^2\),定义“代价”为 \[ \eta\big\langle\nabla f(\mathbf x_t),\mathbf x-\mathbf x_t\big\rangle+\frac{1}{2}\Vert\mathbf x-\mathbf x_t\mathbf\Vert^2 \] 取 argmin 得 \(\mathbf x_{t+1}=\mathbf x_t-\eta\nabla f(\mathbf x_t)\),这就是梯度下降。
我们可以将正则化项扩展为贝格曼距离。令 \(w\) 是 \(1\)-strongly convex 的,由此生成距离函数 \(D\),令“广义学习率”为 \(\alpha\),定义迭代 \[ \mathbf x_{t+1}={\rm argmin}_{\mathbf x}\Big(\alpha\big\langle\nabla f(\mathbf x_t),\mathbf x-\mathbf x_t\big\rangle+V_{\mathbf x_t}(\mathbf x)\Big) \] 这就是镜像梯度下降。
- 镜像梯度下降的代数形式
\(\mathbf x_{t+1}\) 是 \(g(\mathbf x)=\alpha\langle\nabla f(\mathbf x_t),\mathbf x-\mathbf x_t\big\rangle+V_{\mathbf x_t}(\mathbf x)\) 的最小值点,得 \[ \nabla g(\mathbf x_{t+1})=\alpha\nabla f(\mathbf x_t)+\nabla w(\mathbf x_{t+1})-\nabla w(\mathbf x_t)=0 \] 即 \[ \nabla w(\mathbf x_{t+1})=\nabla w(\mathbf x_t)-\alpha\nabla f(\mathbf x_t) \] \(w\) 是强凸的,故 \(\nabla w\) 取遍 \(\mathbb R^n\)(证明略),可以定义它的反函数 \((\nabla w)^{-1}\),故 \[ \mathbf x_{t+1}=(\nabla w)^{-1}\Big(\nabla w(\mathbf x_t)-\alpha\nabla f(\mathbf x_t)\Big) \]
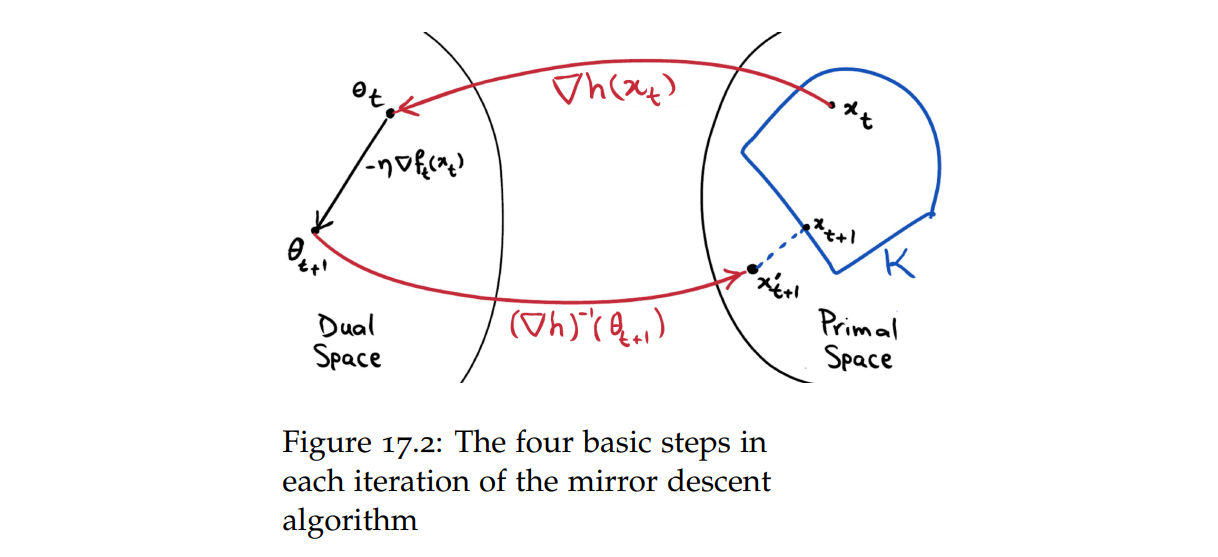
- 视角二:对偶空间
观察代数形式,它可以解释为:
- 将 \(\mathbf x_t\) 映射到对偶空间 \(\nabla w(\mathbf x_t)\)
- 在对偶空间上行走一步 \(-\alpha\nabla f(\mathbf x_t)\),得到 \(\nabla w(\mathbf x_{t+1})\)
- 映射回原空间,得到 \(\mathbf x_{t+1}\)
对偶空间就像原空间的 "mirror",镜像梯度下降由此得名。
【注 1】原始论文对对偶空间的解释大概如下:我们不应将梯度视为向量(原空间中的元素),而应该将其视为线性函数(对偶空间中的元素)。在这种视角下,由于类型不同,\(\mathbf x_t\) 和 \(\nabla f(\mathbf x_t)\) 不应该直接相加,需要先将 \(\mathbf x_t\) 转化到对偶空间上。
【注 2】我查了一车资料,没人解释这个对偶空间除了满足类型论的直觉还有啥实际用途,但是很多讲义都画了那张进出对偶空间的图,可能只是因为比较直观好记。
镜像梯度下降的收敛性
和梯度下降一致:
- 在光滑凸函数上,收敛率 \(O(1/T)\)。
- 在连续凸函数上,收敛率 \(O(1/\sqrt{T})\)。
下面进行具体分析。
光滑凸函数上的镜像梯度下降
\(f(\mathbf x)\) 是凸的,且是 \(L\)-smooth 的,设 \(f(\mathbf x)\) 的最小值是 \(f^*=f(\mathbf x^*)\),从 \(\mathbf x_0\) 出发,进行镜像梯度下降。
- 单调性
\[ \begin{aligned} f(\mathbf x_{t+1}) &\leq f(\mathbf x_t)+\big\langle\nabla f(\mathbf x_t),\mathbf x_{t+1}-\mathbf x_t\big\rangle+\frac{L}{2}\Vert\mathbf x_{t+1}-\mathbf x_t\mathbf\Vert^2 &(\text{光滑函数的二次上界})\\ f(\mathbf x_{t+1})-f(\mathbf x_t) &\leq \big\langle\nabla f(\mathbf x_t),\mathbf x_{t+1}-\mathbf x_t\big\rangle+L V_{\mathbf x_{t}}(\mathbf x_{t+1})\\ \end{aligned} \]
取 \(\alpha\leq \frac{1}{L}\),则 \[ \begin{aligned} f(\mathbf x_{t+1})-f(\mathbf x_t) &\leq \big\langle\nabla f(\mathbf x_t),\mathbf x_{t+1}-\mathbf x_t\big\rangle+\frac{1}{\alpha} V_{\mathbf x_t}(\mathbf x_{t+1})\\ &=\frac{1}{\alpha}\bigg(w(\mathbf x_{t+1})-w(\mathbf x_t)+\big\langle\nabla w(\mathbf x_{t+1}),\mathbf x_t-\mathbf x_{t+1}\big\rangle\bigg)\\ &=-\frac{1}{\alpha}V_{\mathbf x_{t+1}}(\mathbf x_t) \end{aligned} \] 这说明镜像梯度下降一定使函数值减小。
- 收敛性
\[ \begin{aligned} f(\mathbf x_{t+1})&\leq f(\mathbf x_t)-\frac{1}{\alpha}V_{\mathbf x_{t+1}}(\mathbf x_t)\\ &\leq f(\mathbf x^*)+\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf x^*\rangle-\frac{1}{\alpha}V_{\mathbf x_{t+1}}(\mathbf x_t)&(\text{凸函数的性质})\\ f(\mathbf x_{t+1})-f(\mathbf x^*) &\leq \frac{1}{\alpha}\Big(\big\langle\nabla w(\mathbf x_t)-\nabla w(\mathbf x_{t+1}),\mathbf x_t-\mathbf x^*\big\rangle-V_{\mathbf x_t}(\mathbf x_{t+1})\Big)\\ &=\frac{1}{\alpha}\Big(V_{\mathbf x_{t+1}}(\mathbf x^*)-V_{\mathbf x_t}(\mathbf x^*)\Big)&(V\text{的定义}) \end{aligned} \] 取 \(t=0\sim (T-1)\) 求和得 \[ \begin{aligned} \sum_{t=1}^T\Big(f(\mathbf x_t)-f(\mathbf x^*)\Big)\leq \frac{1}{\alpha}\Big(V_{\mathbf x_0}(\mathbf x^*)-V_{\mathbf x_T}(\mathbf x^*)\Big) \end{aligned} \] 设 \(V_{\mathbf x_0}(\mathbf x^*)\leq \Theta\),根据 Jensen 不等式 \[ f(\overline{\mathbf x})-f(\mathbf x^*)\leq \frac{\Theta}{\alpha T} \]
连续凸函数上的镜像梯度下降
\(f(\mathbf x)\) 是凸的,且是 \(\rho\)-Lipschitz 的,设 \(f(\mathbf x)\) 的最小值是 \(f^*=f(\mathbf x^*)\),从 \(\mathbf x_0\) 出发,进行镜像梯度下降。
\[ \begin{aligned} f(\mathbf x_t)-f(\mathbf x^*) &\leq \big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf x^*\big\rangle &\text{(凸性)}\\ &= \big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf x_{t+1}\big\rangle+ \big\langle\nabla f(\mathbf x_t),\mathbf x_{t+1}-\mathbf x^*\big\rangle \\ \alpha\big(f(\mathbf x_{t+1})-f(\mathbf x_t)\big) &\leq \alpha\big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf x_{t+1}\big\rangle+ \big\langle\nabla w(\mathbf x_t)-\nabla w(\mathbf x_{t+1}),\mathbf x_{t+1}-\mathbf x^*\big\rangle \\ &= \alpha\big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf x_{t+1}\big\rangle+ V_{\mathbf x_k}(\mathbf x^*)-V_{\mathbf x_{k+1}}(\mathbf x^*)-V_{\mathbf x_k}(\mathbf x_{k+1}) &(V\text{的定义})\\ &\leq\Big(\alpha\big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf x_{t+1}\big\rangle-\frac{1}{2}\Vert\mathbf x_t-\mathbf x_{t+1}\Vert^2\Big)+V_{\mathbf x_t}(\mathbf x^*)-V_{\mathbf x_{t+1}}(\mathbf x^*)\\ &\leq \frac{\alpha^2}{2}\Vert\nabla f(\mathbf x_t)\Vert^2+V_{\mathbf x_t}(\mathbf x^*)-V_{\mathbf x_{t+1}}(\mathbf x^*) &(\text{递推定义})\\ &=\frac{\alpha^2\rho^2}{2}+V_{\mathbf x_t}(\mathbf x^*)-V_{\mathbf x_{t+1}}(\mathbf x^*) &{(\rho\,\text{-Lipschitz})} \end{aligned} \] 对 \(t=0\sim (T-1)\) 求和得 \[ \alpha\sum_{t=0}^{T-1}\Big(f(\mathbf x_t)-f^*\Big)\leq\frac{T\alpha^2\rho^2}{2}+V_{\mathbf x_0}(\mathbf x^*)-V_{\mathbf x_T}(\mathbf x^*) \] 设 \(V_{\mathbf x_0}(\mathbf x^*)\leq \Theta\),根据 Jensen 不等式 \[ f(\overline{\mathbf x})-f^*\leq\frac{\alpha\rho^2}{2}+\frac{\Theta}{\alpha T} \] 取 \(\alpha=\sqrt{2\Theta/\rho^2T}\) 得 \[ f(\overline{\mathbf x})-f^*\leq\frac{\rho\sqrt{2\Theta}}{\sqrt{T}} \]
* 再谈投影梯度下降
回顾前文的内容:解决带约束优化问题时,投影梯度下降需要计算 \({\rm proj}_S(\mathbf u)\),然而,基于 2-范数的投影可能难以计算或性质较差。转而考虑“贝格曼投影”,根据集合 \(S\) 的形状设计合适的贝格曼距离,可以简化投影的计算,或取得更好的性质。
例如:在概率单纯形 \(\mathcal X=\{\mathbf x\in\mathbb R_+^n\mid\sum_{i=1}^nx_i=1\}\) 上,如果令贝格曼距离为“熵距离”,即令 \(w(\mathbf x)=\sum_{i=1}^nx_i\log x_i\),则对于 \(y\in\mathbb R_+^n\) ,\({\rm proj}_{\mathcal X}(\mathbf y)=\mathbf y/\Vert\mathbf y\Vert_1\)。证明略。
此外,由于熵的梯度在 \(x_i\to 0\) 时发散到无穷,镜像梯度下降不可能到达负区域,这样就保证了\(y\in\mathbb R_+^n\)。该算法也就是所谓的指数梯度下降。
一阶方法的加速
在光滑凸函数上,Nesterov 证明了一阶方法的最优收敛率是 \(1/T^2\),下面我们将给出一个达到此收敛率的算法。
假设目前有 \(f(\mathbf x_0)-f^*\leq 2\epsilon\),我们的目标是得到 \(\mathbf x\) 满足 \(f(\mathbf x)-f^*\leq \epsilon\)。如果这只需要 \(O(1/\sqrt{\epsilon})\) 步,考虑 \(\cdots\to 8\epsilon\to 4\epsilon\to 2\epsilon\to \epsilon\) 的过程,总步数为 \[ O\left(\frac{1}{\sqrt{\epsilon}}+\frac{1}{\sqrt{2\epsilon}}+\frac{1}{\sqrt{4\epsilon}}+\cdots\right)=O\left(\frac{1}{\sqrt{\epsilon}}\right) \] 那么收敛率也就是 \(1/T^2\)。
直觉
在梯度下降中:
- 对于光滑凸函数,\(f(\mathbf x_{t+1})-f(\mathbf x_t)\leq -\frac{\eta}{2}\Vert\nabla f(\mathbf x_t)\Vert^2\),梯度越大,下降越快。
- 对于连续凸函数,\(f(\overline{\mathbf x})-f^*\leq\frac{\eta\rho^2}{2}+\frac{\Theta}{2\eta T}\),梯度(也就是 \(\rho\))越小,误差项越小。
理想化地,假设存在常数 \(K\),使我们的函数梯度模长要么小于 \(K\),要么大于 \(K\)。
若梯度模长恒大于 \(K\),运行“光滑凸函数上的梯度下降”。需要下降的高度为 \(\epsilon\),每次至少下降 \(\frac{\eta K^2}{2}\),故所需步数为 \(O(\frac{\epsilon}{K^2})\)。
若梯度模长恒小于 \(K\),运行“连续凸函数上的梯度下降”。\(f(\overline{\mathbf x})-f^*\leq\frac{K\sqrt{\Theta}}{\sqrt{T}}\leq \epsilon\),所需步数为 \(O(\frac{K^2}{\epsilon^2})\)。
取最佳的 \(K\),满足 \(K^2=\epsilon^{3/2}L^{1/2}\),然后在两种算法中取最好的,可得步数 \(O(1/\sqrt{\epsilon})\)。
当然,这只是一个很粗略的设计,因为实际上函数的梯度可能一会小于 \(K\),一会大于 \(K\)。
线性耦合
\(f\) 凸且 \(L\)-smooth,初始点为 \(\mathbf x_0\),设目前有 \(f(\mathbf x_0)-f^*\leq 2\epsilon\),我们的目标是得到 \(\mathbf x\) 满足 \(f(\mathbf x)-f^*\leq \epsilon\)。
令 \(\tau,\eta,\alpha\) 为常数(其中 \(\tau\) 是耦合比率),考虑如下递推: \[ \begin{aligned} \mathbf y_{t+1}&=\mathbf x_t-\eta\nabla f(\mathbf x_t)\\ \mathbf z_{t+1}&=\mathbf z_t-\alpha\nabla f(\mathbf x_t)\\ \mathbf x_t&=\tau\mathbf z_t+(1-\tau)\mathbf y_t\\ \end{aligned} \]
- 准备
在“光滑凸函数上的梯度下降“中,我们证明了,若 \(\mathbf x_{t+1}=\mathbf x_t-\eta\nabla f(\mathbf x_t)\),且 \(\eta\leq\frac{1}{L}\),则 \[ \frac{\eta}{2}\Vert\nabla f(\mathbf x_t)\Vert^2\leq f(\mathbf x_t)-f(\mathbf x_{t+1}) \] 在“连续凸函数上的梯度下降“中,我们证明了,若 \(\mathbf x_{t+1}=\mathbf x_t-\alpha\mathbf q\),则 \[ \big\langle\mathbf q,\mathbf x_t-\mathbf x^*\big\rangle = \frac{1}{2\alpha}\Big( \alpha^2\Vert\mathbf q\Vert^2 +\Vert\mathbf x_t-\mathbf x^*\Vert^2 -\Vert\mathbf x_{t+1}-\mathbf x^*\Vert^2 \Big)\\ \]
- 收敛性分析
\[ \begin{aligned} f(\mathbf x_t)-f(\mathbf x^*) &\leq \big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf x^*\big\rangle &\text{(凸性)}\\ &= \big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf z_t\big\rangle+\big\langle\nabla f(\mathbf x_t),\mathbf z_t-\mathbf x^*\big\rangle \end{aligned} \]
对于右侧 \[ \begin{aligned} \big\langle\nabla f(\mathbf x_t),\mathbf z_t-\mathbf x^*\big\rangle&= \frac{1}{2\alpha}\left( \alpha^2\Vert\nabla f(\mathbf x_t)\Vert^2 +\Vert\mathbf z_t-\mathbf x^*\Vert^2 -\Vert\mathbf z_{t+1}-\mathbf x^*\Vert^2 \right)\\ &\leq \frac{1}{2\alpha}\Big( \frac{\alpha^2}{\eta}\big(f(\mathbf x_t)-f(\mathbf y_{t+1})\big) +\Vert\mathbf z_t-\mathbf x^*\Vert^2 -\Vert\mathbf z_{t+1}-\mathbf x^*\Vert^2 \Big) \end{aligned} \] 对于左侧 \[ \begin{aligned} \big\langle\nabla f(\mathbf x_t),\mathbf x_t-\mathbf z_t\big\rangle&=\frac{1-\tau}{\tau}\big\langle\nabla f(\mathbf x_t),\mathbf y_t-\mathbf x_t\big\rangle&(\mathbf x,\mathbf y,\mathbf z\,\text{的定义})\\ &\leq\frac{1-\tau}{\tau}\big(f(\mathbf y_t)-f(\mathbf x_t)\big)&\text{(凸性)} \end{aligned} \] 令 \(\frac{1-\tau}{\tau}=\frac{\alpha}{2\eta}\),将两者相加得 \[ f(\mathbf x_t)-f(\mathbf x^*) \leq \frac{\alpha}{\eta}\big(f(\mathbf y_t)-f(\mathbf y_{t+1})\big) +\frac{1}{2\alpha}\big( \Vert\mathbf z_t-\mathbf x^*\Vert^2 -\Vert\mathbf z_{t+1}-\mathbf x^*\Vert^2 \big) \] 刚好分成两块可以裂项相消,求和得 \[ \sum_{t=1}^T\big(f(\mathbf x_t)-f^*\big)\leq \frac{\alpha}{\eta}\big(f(\mathbf x_0)-f^*\big)+\frac{1}{2\alpha}\Vert\mathbf x_0-\mathbf x^*\Vert^2 \] 设 \(\Vert\mathbf x_0-\mathbf x^*\Vert^2\leq \Theta\),根据 Jensen 不等式 \[ f(\overline{\mathbf x})-f^*\leq \frac{1}{T}\left(\frac{2\epsilon\alpha}{\eta}+\frac{\Theta}{2\alpha}\right) \] 令 \(\eta=\frac{1}{L},\alpha=\sqrt{\frac{\Theta}{L\epsilon}}\),则 \[ f(\overline{\mathbf x})-f^*\leq\frac{3\sqrt{\Theta L\epsilon}}{T} \] 令 \(T=3\sqrt{\Theta L/\epsilon}=O(1/\sqrt{\epsilon})\) 就能做到 \(f(\overline{\mathbf x})-f^*\leq \epsilon\) 了。
根据前文的分析,多次重复该算法(并设定不同的 \(\alpha,\tau\))使“高度”不断减半,即可得到 \(O(1/T^2)\) 的收敛率。
【注 1】论文将该算法解释为 GD 和 MD 的“线性耦合”,并证明了带 Bregman divergence 的版本,但这是不必要的。算法其实只是“光滑函数上的梯度下降”和“连续函数上的梯度下降”的耦合。
【注 2】迭代中 \(\mathbf z_{t+1}=\mathbf z_t-\alpha\nabla f(\mathbf x_t)\) 一步非常奇怪,它在 \(\mathbf z_t\) 处借用了梯度 \(\nabla f(\mathbf x_t)\),这没法从 GD 的视角解释。论文将其解释为 Mirror Step,我没看懂它和 MD 有什么联系,但反正能证就对了。